Introduction

Could you answer this by just using your intuition? The problem is to compute an approximate probability that in a classroom of n students or let’s say in your class at least two students have the same birthday. What answer is your intuition suggesting? Feel free to comment below and compare them with the actual results.

Let’s begin the mathematical analysis of this problem.

Do we need Assumptions?

Let’s assume that all 365 possible birthdays are equally likely. Ignored the leap years for simplicity, but the answer would be the same for leap years too. Also, we all know that real-life birthday distributions are not uniform, since not all dates are equally likely, these irregularities have little effect on the analysis. Actually, the uniform distribution of birth dates would be the worst case.

Mathematical Analysis

The goal is to compute P(A), the probability that at least two students in the classroom have the same birthday. However, it is simpler to calculate P(A′), the probability that no two students in the classroom have the same birthday. Then, because A and A′ are the only two possibilities and are also mutually exclusive, therefore P(A) = 1 − P(A′). For this analysis let’s take the classroom strength to be 60 and then the process can be generalized for n students.

Let us number the 60 students from 1 to 60. The event that all 60 students have different birthdays is the same as the event that student 2 does not have the same birthday as student 1, and that student 3 does not have the same birthday as either student 1 or student 2, and so on, and finally that student 60 does not have the same birthday as any of students 1 through 59. Let these events respectively be called “Event 2”, “Event 3”, and so on. Now we need to add an “Event 1”, corresponding to the event of student 1 having a birthday, which occurs with probability 1.

This conjunction of events may be computed using conditional probability. The probability of Event 2 is 364/365, as student 2 may have any birthday other than the birthday of student 1. Similarly, the probability of Event 3 given that Event 2 occurred is 363/365, as student 3 may have any of the birthdays not already taken by students 1 and 2. This continues until finally the probability of Event 60 given that all preceding events occurred is 306/365. Finally, the principle of conditional probability implies that P(A′) is equal to the product of these individual probabilities:

P(A′) = 365365 ✖364365 ✖363365 ….. ✖307365 ✖306365

P(A′) = (1365)60 ✖ 365 ✖ 364 ✖ 363 …… ✖ 307 ✖ 306

P(A’) will come out to be approximately equal to 0.006.

Therefore, P(A) = 1 − 0.006 = 0.994 i.e. 99.4%.

This process can be generalized for n students or n people in a group.

Let p(n) be the probability of at least two of the n people sharing a birthday.

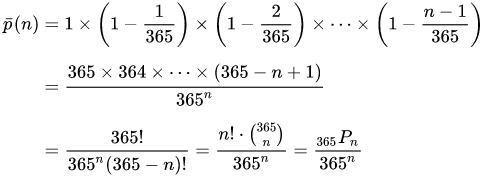
The following graph shows the different probabilities for different values of n.

Conclusion

Almost 100% chance and to be exact 99.4% chance that at least two of your classmates can have the same birthday if the classroom strength is 60. Similarly, in a classroom of 23 students, the probability of a shared birthday exceeds 50%, while a classroom of 70 has a 99.9% chance of a shared birthday. Since there are only 366 possible birthdays, including February 29, and the number of students reaches 367, then the probability reaches 100%.

The birthday problem is just one example where math can show that things that seem impossible, like the same person winning the lottery twice, actually aren’t unlikely at all. Sometimes coincidences aren’t as coincidental as they seem.

Real World Application

Real-world applications for the birthday problem includes a cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of finding a collision for a hash function, as well as calculating the approximate risk of a hash collision existing within the hashes of a given size of the population. Additional information regarding this is provided in the external links.

References

You can refer to the below-listed sources for more details:

Link: https://www.khanacademy.org/math/statistics-probability/counting-permutations-and-combinations/combinatorics-probability/v/birthday-probability-problem Link: https://ed.ted.com/lessons/check-your-intuition-the-birthday-problem-david-knuffke#watch Link: https://en.wikipedia.org/wiki/Birthday_problem